注意

点击此处下载完整示例代码，或通过 Binder 在浏览器中运行此示例

回归

以下示例展示了如何使用 auto-sklearn 拟合一个简单的回归模型。

from pprint import pprint

import sklearn.datasets
import sklearn.metrics

import autosklearn.regression
import matplotlib.pyplot as plt

数据加载

X, y = sklearn.datasets.load_diabetes(return_X_y=True)

X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(
    X, y, random_state=1
)

构建并拟合回归器

automl = autosklearn.regression.AutoSklearnRegressor(
    time_left_for_this_task=120,
    per_run_time_limit=30,
    tmp_folder="/tmp/autosklearn_regression_example_tmp",
)
automl.fit(X_train, y_train, dataset_name="diabetes")

AutoSklearnRegressor(ensemble_class=<class 'autosklearn.ensembles.ensemble_selection.EnsembleSelection'>,
                     per_run_time_limit=30, time_left_for_this_task=120,
                     tmp_folder='/tmp/autosklearn_regression_example_tmp')

查看 auto-sklearn 找到的模型

print(automl.leaderboard())

          rank  ensemble_weight               type      cost  duration
model_id
25           1             0.46                sgd  0.436679  0.701417
6            2             0.32     ard_regression  0.455042  0.779423
27           3             0.14     ard_regression  0.462249  0.826378
11           4             0.02      random_forest  0.507400  9.763534
7            5             0.06  gradient_boosting  0.518673  1.450713

获取最终集成模型的得分

训练完估计器后，我们现在可以量化拟合的优劣。一种可能的方法是使用 R2 分数。该值的范围在 -inf 到 1 之间，其中 1 是最优值。一个预测数据均值的虚拟估计器的 R2 分数为 0。

train_predictions = automl.predict(X_train)
print("Train R2 score:", sklearn.metrics.r2_score(y_train, train_predictions))
test_predictions = automl.predict(X_test)
print("Test R2 score:", sklearn.metrics.r2_score(y_test, test_predictions))

Train R2 score: 0.5944780427522034
Test R2 score: 0.3959585042866587

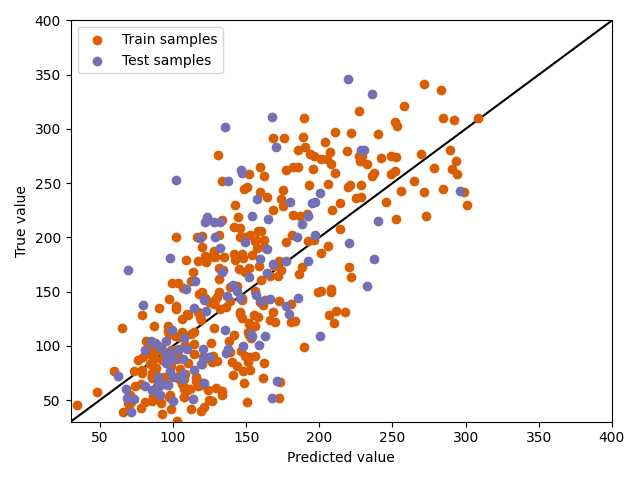
绘制预测结果

此外，我们现在可以直观地检查预测结果。我们绘制真实值与预测值的对比图，并展示训练集和测试集上的结果。对角线上的点表示完美的预测。对角线下方的点表示模型高估了（预测值高于真实值），对角线上方的点表示低估了（预测值低于真实值）。

plt.scatter(train_predictions, y_train, label="Train samples", c="#d95f02")
plt.scatter(test_predictions, y_test, label="Test samples", c="#7570b3")
plt.xlabel("Predicted value")
plt.ylabel("True value")
plt.legend()
plt.plot([30, 400], [30, 400], c="k", zorder=0)
plt.xlim([30, 400])
plt.ylim([30, 400])
plt.tight_layout()
plt.show()
example regression

脚本总运行时间： ( 2 分钟 3.004 秒)

画廊由 Sphinx-Gallery 生成